1. Proposición negativa o negación (~).
Son aquellas proposiciones que hacen uso del adverbio negativo NO o sus expresiones equivalentes.
Ejemplos:
- El perro no ladra.
- No es el caso de que el perro ladre.
- No es cierto que el perro ladre.
- Es falso que el perro ladre.
- No ocurre que el perro ladre.
En general, la negación puede reducirse a la palabra NO, a la que simbolizaremos mediante ~. Por convención, se coloca siempre a la izquierda de la proposición que niega. Por tanto, si representamos la proposición El perro ladra mediante p, su negación se representaría como ~p y su tabla de verdad resultaría la siguiente:
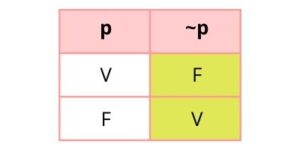
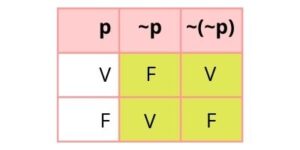
2. Proposición conjuntiva o conjunción (∧).
Son aquellas proposiciones que se relacionan con el conector lógico y, o sus expresiones equivalentes.
Ejemplos:
- Tesla fue biólogo y Newton físico.
- El 13 es número impar, además es primo.
- La actriz es bella pero realista.

3. Proposición disyuntiva o disyunción (v).
Son aquellas proposiciones que se relacionan mediante el conectivo lógico ‘o’, u otras expresiones equivalentes.
Ejemplos:
- Hace frío o está lloviendo.
- 10 es par o múltiplo de 2.
- Está despierto o está durmiendo.
En los ejemplos iniciales, el uso del conectivo «o» señala que al menos una de las proposiciones es válida (sin excluir la posibilidad de que ambas lo sean simultáneamente). Sin embargo, en el tercer caso, el empleo de
l «o» excluye que ambas proposiciones ocurran al mismo tiempo. De este modo, una proposición disyuntiva puede clasificarse según este criterio:
3.1. Inclusiva o débil (v)
Es aquella en la cual se consideran las posibles ocurrencias simul
táneas o individuales de las proposiciones componentes.
Ejemplo:
Carlos es matemático o poeta. Analicemos los valores de verdad para esta proposición.
Resolución El conectivo «o» nos indica
que al menos una de las proposiciones es verdadera y se simboliza con el signo «v». Por ejemplo, si «p» es la proposición «Carlos es matemático» y «q» es la
proposición «Carlos es poeta», la disyuntiva de ambas es «p v q» (que se lee «p y/o q»).
Puesto que la disyuntiva de dos proposiciones cualquiera indica la verdad de al menos una de ellas, la proposición compuesta resultante es verdadera si efectivamente al menos una de ellas es verdadera.
Esto se puede analizar en la siguiente tabla:

3.2. Exclusiva o fuerte (Δ, ∨̇)
Esta disyuntiva excluye la posibilidad de ocurrencia simultánea de ambas proposiciones componentes.
Ejemplo:
Si consideramos con «r» a la proposición simple «Estás despierto» y con «s» la proposición simple «Estás durmiendo», la disyuntiva se simboliza con el signo Δ. Luego, (r Δ s) será: «O estás despierto o estás durmiendo». Elabore su tabla de verdad.
Resolución Dado que se excluye la ocurrencia simultánea de ambas proposiciones, la proposición resultante será verdadera solo en el caso que una de las componentes sea verdadera y la otra sea falsa. Los valores que pueda asumir «r Δ s» están definidos en la siguiente tabla de verdad.

4. Condicional (→).
Son aquellas proposiciones que se relacionan mediante el conectivo lógico «Si…entonces…» o sus expresiones equivalentes.
- Si estudias, entonces ingresarás a la universidad.
- Si pago la entrada, entonces ingreso al cine.
El conectivo «Si…entonces…» se simboliza mediante el signo →, el cual se escribe entre las dos proposiciones relacionadas. Por ejemplo, si p representa la proposición simple «pago la entrada» y q la proposición simple «ingreso al cine», entonces la condicional se simboliza como p → q.
La proposición condicional consta de dos partes: el antecedente y el consecuente: p → q Antecedente: p Consecuente: q
El propósito de este conectivo es expresar que si la proposición antecedente es verdadera, también lo será la proposición consecuente. Es decir, basta con que el antecedente sea verdadero para que el consecuente también sea verdadero. Por lo tanto, una condicional será falsa solo si el antecedente es verdadero y el consecuente es falso.
La tabla de verdad correspondiente a una proposición condicional es la que se muestra a continuación:
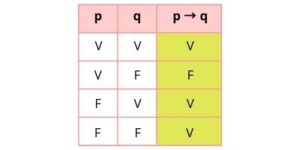
La proposición condicional puede ser:
Directa El antecedente y consecuente van en este orden, respectivamente.
Ejemplos:
-
Si llueve, entonces me mejoraré. Antecedente: Si llueve Consecuente: Me mejoraré
-
Nació en Ica, de modo que es iqueño. Antecedente: Nació en Ica Consecuente: Es iqueño
-
Mary tiene fiebre, por lo tanto está enferma. Antecedente: Mary tiene fiebre Consecuente: Está enferma
Inversa
En una proposición inversa, se invierten el consecuente y el antecedente.
Ejemplos:
1. Ingresaste porque estudiaste.
-
-
Consecuente: Ingresaste
-
Antecedente: Estudiaste
-
2. Entrarás al cine solo si pagas.
-
Consecuente: Entrarás al cine
-
Antecedente: Pagas
5. Bicondicional (↔).
Son aquellas proposiciones que se relacionan mediante el conectivo lógico «si y solo si» o expresiones equivalentes.
Ejemplos:
- Un ángulo es recto, si y solo si su medida es 90°.
- La educación mejorará cuando, y solo cuando, se tenga una sociedad justo.
El conector «si y solo si» se simboliza con signo ↔ , e indica que ambas proposiciones son equivalentes.

A continuación te muestro un resúmen de todas las tablas en una sola:
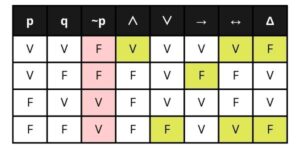
Puedes descargar todas las tablas a tu celular directamente en formatos PDF y WORD haciendo click en las imágenes imágenes.





