Título: ¡El Secreto de los Triángulos al Descubierto! El Teorema de Pitágoras
¿Sabías que una fórmula matemática de hace más de 2,500 años es fundamental para la construcción, el diseño y hasta para los videojuegos? ¡Es el Teorema de Pitágoras y es más fácil de lo que piensas!
El teorema se aplica a cualquier triángulo rectángulo (el que tiene un ángulo de 90°) y establece una relación increíblemente útil entre sus lados.
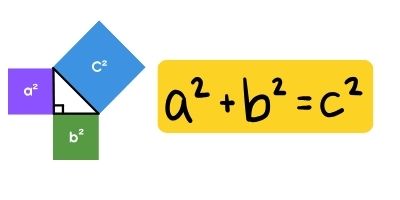
La Fórmula Mágica:
¡No te asustes! Significa simplemente que si tomas las longitudes de los dos lados más cortos (los catetos, llamados ‘a’ y ‘b’) y las elevas al cuadrado, la suma es igual al cuadrado del lado más largo (la hipotenusa, ‘c’).
- a y b: Los lados que forman el ángulo recto.
- c: El lado opuesto al ángulo recto, ¡siempre el más largo!
Visualmente, significa que el área del cuadrado que puedes formar con la hipotenusa es igual a la suma de las áreas de los cuadrados de los otros dos lados.
¿Para Qué Sirve en la Vida Real?
Imagina que tienes una escalera de 5 metros (c) y la apoyas contra una pared. Si la base de la escalera está a 3 metros de la pared (b), ¿qué tan alto llegará en la pared (a)?
1. Usamos la fórmula:
2. Calculamos los cuadrados:
3. Restamos:
4. Sacamos la raíz cuadrada:
5. ¡El resultado es a = 4 metros!
Así de fácil puedes calcular distancias sin tener que medirlas directamente.
El Teorema de Pitágoras es una prueba de cómo las matemáticas nos ayudan a entender y a construir nuestro mundo.



