Cuando estudiamos triángulos en geometría, hay ciertos elementos que aparecen una y otra vez por su importancia. Hoy vamos a hablar de las líneas notables y los puntos notables de un triángulo, conceptos clave para entender su estructura y resolver muchos ejercicios.
¿Qué son las líneas notables?
Las líneas notables son segmentos especiales que se trazan desde un vértice del triángulo hacia algún punto del lado opuesto (o su prolongación). Las principales son:
- Mediatriz
- Mediana
- Altura
- Bisectriz
¿Y los puntos notables?
Como ya viste, cada grupo de líneas notables se cruza en un punto especial. Estos son los puntos notables de un triángulo:
| Punto Notable | Formado por | Propiedad Principal |
|---|---|---|
| Circuncentro | Mediatrices | Centro del círculo que pasa por los 3 vértices |
| Incentro | Bisectrices | Centro del círculo que toca los 3 lados |
| Baricentro | Medianas | Centro de masa del triángulo |
| Ortocentro | Alturas | Punto donde se cruzan las alturas |
1. Mediatriz
-
Es la recta perpendicular a un lado del triángulo que lo corta en su punto medio.
-
No necesariamente pasa por un vértice.
-
Las tres mediatrices se cortan en un punto llamado circuncentro.
-
El circuncentro es el centro del círculo circunscrito al triángulo (el que pasa por sus tres vértices).
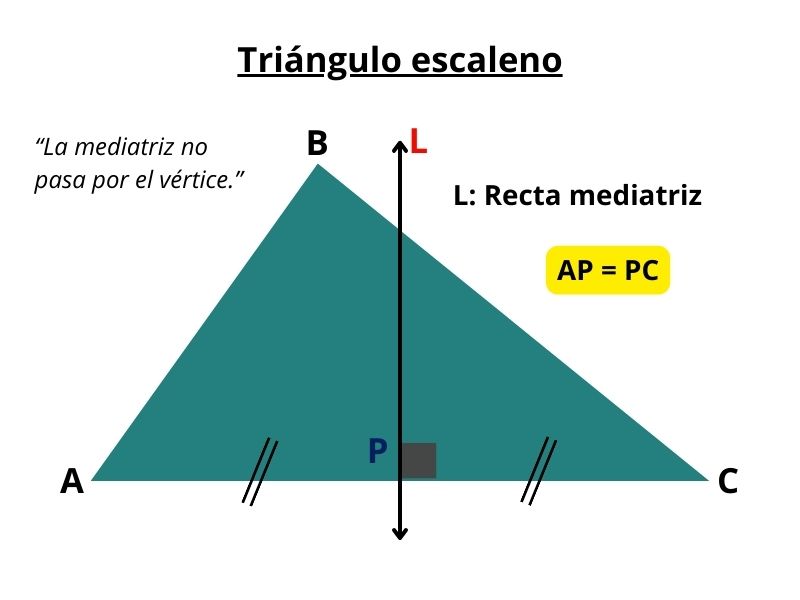
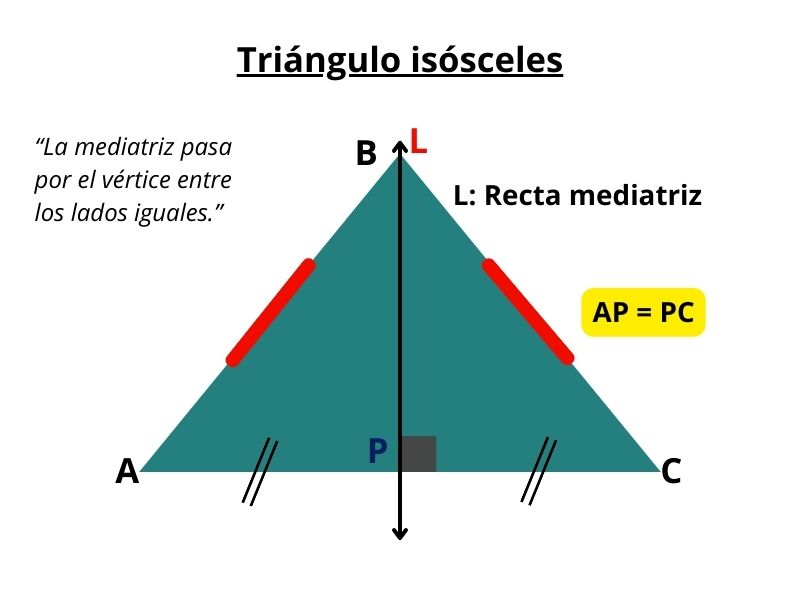
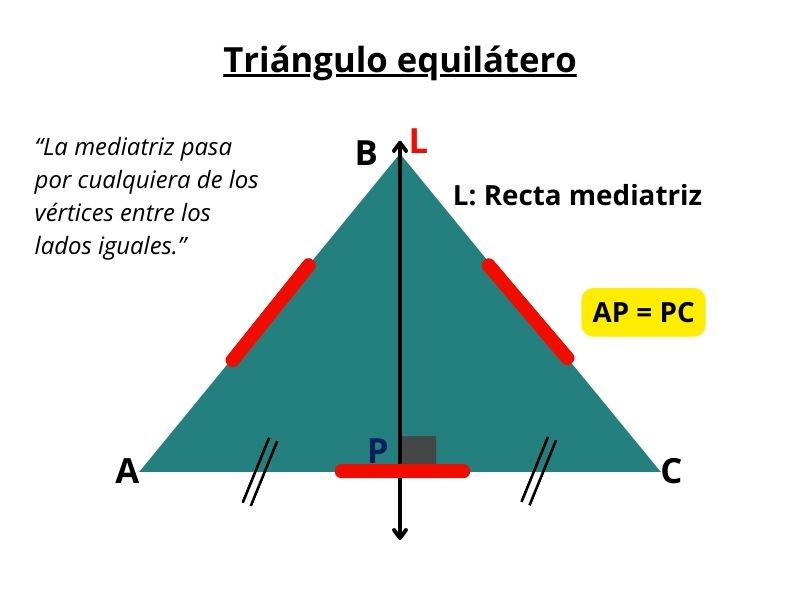
En todo triángulo, las mediatrices de sus tres lados son concurrentes (se cruzan en el mismo punto)

1.1. EL CIRCUNCENTRO (O)
Es el centro de la circunferencia circunscrita a un triángulo.
Las mediatrices de los tres lados concurren en el circuncentro
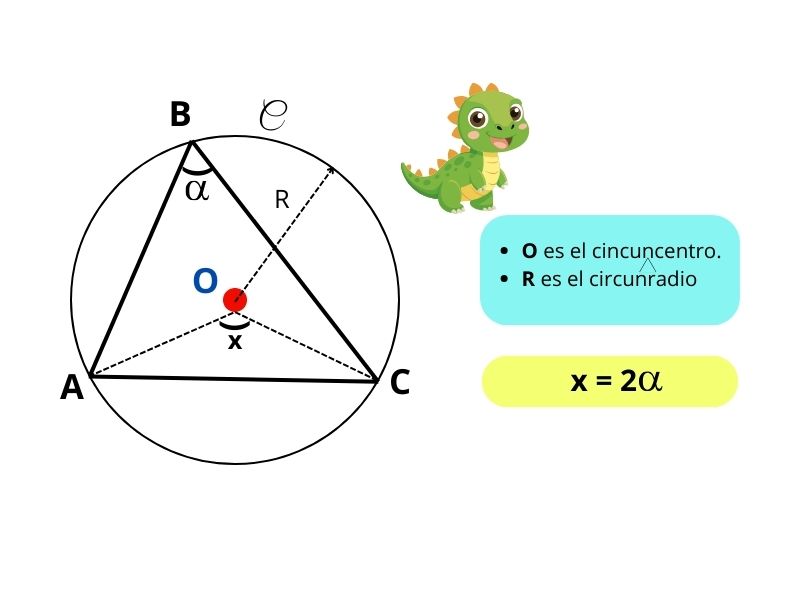
Situaciones importantes
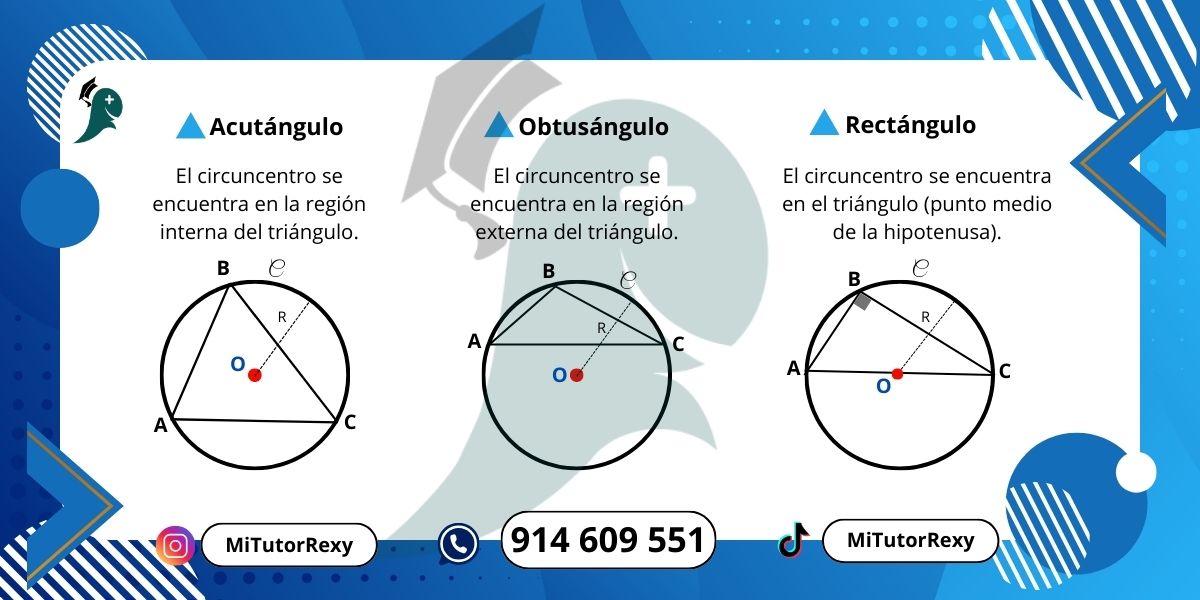
Ejercicios sobre el Circuncentro →
2. Mediana
-
Es el segmento que une un vértice con el punto medio del lado opuesto.
-
Cada triángulo tiene tres medianas.
-
Se intersectan en un punto llamado baricentro.
-
El baricentro es el centro de masa del triángulo y divide cada mediana en una razón 2:1.
3. Bisectriz
-
Es el segmento que parte de un vértice y divide el ángulo en dos partes iguales.
-
Las tres bisectrices se cortan en el incentro.
-
El incentro es el centro del círculo inscrito, que toca los tres lados del triángulo.
4. Altura
-
Es el segmento perpendicular que va de un vértice al lado opuesto (o su prolongación).
-
Representa la “altura” real del triángulo desde ese vértice.
-
Las alturas se intersectan en el ortocentro.
¿Y los puntos notables?
Como ya viste, cada grupo de líneas notables se cruza en un punto especial. Estos son los puntos notables de un triángulo:
¿Por qué son importantes?
Estos puntos y líneas no solo aparecen en teoría: también son fundamentales para resolver problemas de geometría, encontrar centros de figuras, calcular áreas, y aplicar propiedades en triángulos notables como los equiláteros, isósceles y escalenos.
Además, ¡tienen un montón de aplicaciones prácticas! Por ejemplo, el baricentro se usa en física para determinar el equilibrio de una figura, y el circuncentro se puede usar en ingeniería para ubicar equidistancias.
Un tip para memorizar:
Si estás estudiando para un examen, recuerda esta frase:
«MeBiMeAl» = Mediatriz – Bisectriz – Mediana – Altura,
cada una va con su punto:
Ci-In-Ba-Or → Circuncentro, Incentro, Baricentro, Ortocentro.
Si te pareció útil, ¡compártelo o deja tus dudas en los comentarios! Y si quieres practicar ejercicios sobre este tema o necesitas ayuda personalizada, puedes escribirme para agendar una asesoría. 😉



